


Next: References
Up: Structure Inversion Program
Previous: Structure Inversion Program
The principal inversion procedure is based on a perturbation theory
derived from a variational principal for adiabatic stellar pulsations
and is set up to measure deviations of seismic parameters from a
spherically-symmetrical reference solar model.
Our initial analysis of the frequency data will restrict these studies to
axisymmetric deviations from the model, the axis of symmetry
coinciding with the axis of solar rotation. The axisymmetric perturbations
can be obtained by inverting averages over groups of modes; this
significantly reduces both the computational time and the formal errors of the
inversion results. These inversions will be done on a regular basis (say, monthly),
in the data analysis `pipeline'.
Important experience has been gained from determination of the
axisymmetric structure by the inversions of the BBSO data.
Capability for studying nonaxisymmetric perturbations seismologically will be sensitive to
the quality of the data.
However, most questions addressed in this Program deal with the
spherically-symmetric component of the deviation from the standard solar model.
These deviations are determined from the shifts of frequencies of the
axisymmetric modes with respect to model frequencies,
or from the shifts of the mean frequencies of mode multiplets.
For inversions of this type the linearized integral equations relating
frequency perturbations 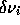 , to variations of the solar structure
are derived from a variational principle. The equations are transformed to
depend on a chosen pair of deviation variables (
, to variations of the solar structure
are derived from a variational principle. The equations are transformed to
depend on a chosen pair of deviation variables (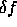 and
and 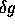 )
that are assumed to be functions of radius r alone (e.g. Kosovichev, 1992), yielding
)
that are assumed to be functions of radius r alone (e.g. Kosovichev, 1992), yielding
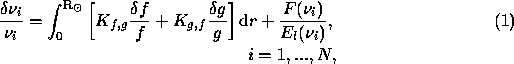
where 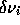 is the frequency difference between the
eigenfrequency,
is the frequency difference between the
eigenfrequency, 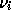 , of a solar model and the corresponding frequency of the
Sun,
, of a solar model and the corresponding frequency of the
Sun, 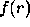 and
and 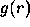 are structure parameters,
are structure parameters,
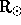 is the radius of the Sun, and
is the radius of the Sun, and 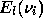 is the
mode inertia. The arbitrary function
is the
mode inertia. The arbitrary function 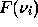 is added to take into account
the surface effects. The suffix i labels the modes; N is the total number
of modes in a data set.
is added to take into account
the surface effects. The suffix i labels the modes; N is the total number
of modes in a data set.
The structure parameters, f and g, can be of two
types: `primary', e.g. the density, 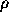 , and the adiabatic exponent,
, and the adiabatic exponent, 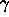 ,
or `secondary', e.g. the hydrogen abundance,
X, and the heavy element abundance, Z. For the `primary' parameters Eq. (1)
is derived using only basic assumptions about solar structure:
spherical symmetry and hydrostatic equilibrium; whereas additional structure equations
have to be considered for the 'secondary' parameters.
In particular, we plan to use
the equation
of state in the form
,
or `secondary', e.g. the hydrogen abundance,
X, and the heavy element abundance, Z. For the `primary' parameters Eq. (1)
is derived using only basic assumptions about solar structure:
spherical symmetry and hydrostatic equilibrium; whereas additional structure equations
have to be considered for the 'secondary' parameters.
In particular, we plan to use
the equation
of state in the form 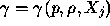 , where
, where 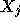 are
element abundances.
are
element abundances.
Two basic inversion procedures, Optimally Localized Averaging (OLA) and
Regularized Least Squares (RLS)
data fitting, have been developed for the structure inversion pipeline.
Both methods essentially subtract from the 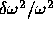 data
a quantity
data
a quantity 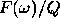 describing unknown surface effects.
The OLA technique will be most commonly used in the project. It consists of constructing
linear combinations of Eq. (1) for a set of
observed modes that provide localized averages of the structure parameters f and g
(e.g. Backus & Gilbert, 1967):
describing unknown surface effects.
The OLA technique will be most commonly used in the project. It consists of constructing
linear combinations of Eq. (1) for a set of
observed modes that provide localized averages of the structure parameters f and g
(e.g. Backus & Gilbert, 1967):
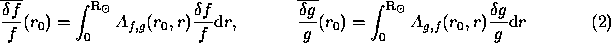
in the vicinity of 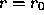 .
The spatial resolution of the averages can be characterized by the central
coordinate and the resolution scale of the averaging kernels. These quantities,
`centre' and `spread', usually represent some integral measure of the kernels
in order to account for effects asymmetry and sidelobes.
.
The spatial resolution of the averages can be characterized by the central
coordinate and the resolution scale of the averaging kernels. These quantities,
`centre' and `spread', usually represent some integral measure of the kernels
in order to account for effects asymmetry and sidelobes.
Selections of the localized averaging kernels for u and the results of a test
inversion of the set of modes, described in the next section
are shown in Fig. 2.
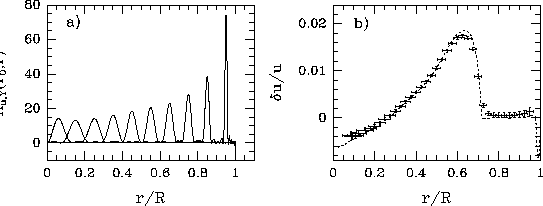
Figure 2: a) Localized averaging kernels, 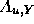 , that
are linear combinations of the corresponding seismic kernels
, that
are linear combinations of the corresponding seismic kernels 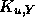 ; b)
Optimally localized averages of the difference
; b)
Optimally localized averages of the difference 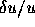 between proxy model 4 and
reference model 1 of Christensen-Dalsgaard et al. (1993)
inferred from the adiabatic frequency differences of the mode set defined
in the text, and the error estimates of IPHIR and BBSO data.
The horizontal bars represent the resolution lengths
(widths of the averaging kernels); the vertical bars represent standard
errors. The dotted curves are the actual differences. (Gough & Kosovichev, 1993)
between proxy model 4 and
reference model 1 of Christensen-Dalsgaard et al. (1993)
inferred from the adiabatic frequency differences of the mode set defined
in the text, and the error estimates of IPHIR and BBSO data.
The horizontal bars represent the resolution lengths
(widths of the averaging kernels); the vertical bars represent standard
errors. The dotted curves are the actual differences. (Gough & Kosovichev, 1993)
If deviations of structure properties are represented in parametric form, then
the unknown parameters can be evaluated from the helioseismic equations (5) using
a least-squares technique. Kosovichev (1993) applied this calibration
technique to determine the helium
abundance and the depth of the convection zone.
The nonspherical axisymmetric perturbations can be considered in the
parametric form:
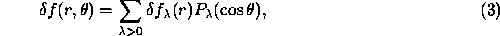
where 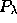 are Legendre polynomials. In this case radial functions
are Legendre polynomials. In this case radial functions
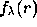 are determined by inverting so-called `a-coefficients',
expansions of the symmetrical part of split-multiplet frequencies into
a set of orthogonal functions of azimuthal order m. The integral equations
relating the even a-coefficients to
are determined by inverting so-called `a-coefficients',
expansions of the symmetrical part of split-multiplet frequencies into
a set of orthogonal functions of azimuthal order m. The integral equations
relating the even a-coefficients to 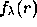 are essentially
identical to Eq. (1) (e.g. Gough, 1993). Therefore, it is proposed to develop
a unified inversion procedure for determining spherical and aspherical
components of the solar structure.
are essentially
identical to Eq. (1) (e.g. Gough, 1993). Therefore, it is proposed to develop
a unified inversion procedure for determining spherical and aspherical
components of the solar structure.



Next: References
Up: Structure Inversion Program
Previous: Structure Inversion Program
Alexander Kosovichev
Sun Aug 6 19:04:23 BST 1995
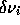 , to variations of the solar structure
are derived from a variational principle. The equations are transformed to
depend on a chosen pair of deviation variables (
, to variations of the solar structure
are derived from a variational principle. The equations are transformed to
depend on a chosen pair of deviation variables (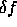 and
and 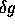 )
that are assumed to be functions of radius r alone (e.g. Kosovichev, 1992), yielding
)
that are assumed to be functions of radius r alone (e.g. Kosovichev, 1992), yielding
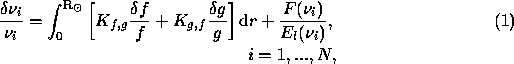
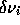 is the frequency difference between the
eigenfrequency,
is the frequency difference between the
eigenfrequency, 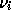 , of a solar model and the corresponding frequency of the
Sun,
, of a solar model and the corresponding frequency of the
Sun, 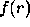 and
and 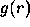 are structure parameters,
are structure parameters,
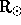 is the radius of the Sun, and
is the radius of the Sun, and 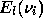 is the
mode inertia. The arbitrary function
is the
mode inertia. The arbitrary function 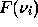 is added to take into account
the surface effects. The suffix i labels the modes; N is the total number
of modes in a data set.
is added to take into account
the surface effects. The suffix i labels the modes; N is the total number
of modes in a data set.
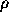 , and the adiabatic exponent,
, and the adiabatic exponent, 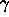 ,
or `secondary', e.g. the hydrogen abundance,
X, and the heavy element abundance, Z. For the `primary' parameters Eq. (1)
is derived using only basic assumptions about solar structure:
spherical symmetry and hydrostatic equilibrium; whereas additional structure equations
have to be considered for the 'secondary' parameters.
In particular, we plan to use
the equation
of state in the form
,
or `secondary', e.g. the hydrogen abundance,
X, and the heavy element abundance, Z. For the `primary' parameters Eq. (1)
is derived using only basic assumptions about solar structure:
spherical symmetry and hydrostatic equilibrium; whereas additional structure equations
have to be considered for the 'secondary' parameters.
In particular, we plan to use
the equation
of state in the form 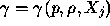 , where
, where 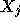 are
element abundances.
are
element abundances.
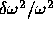 data
a quantity
data
a quantity 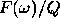 describing unknown surface effects.
The OLA technique will be most commonly used in the project. It consists of constructing
linear combinations of Eq. (1) for a set of
observed modes that provide localized averages of the structure parameters f and g
(e.g. Backus & Gilbert, 1967):
describing unknown surface effects.
The OLA technique will be most commonly used in the project. It consists of constructing
linear combinations of Eq. (1) for a set of
observed modes that provide localized averages of the structure parameters f and g
(e.g. Backus & Gilbert, 1967):
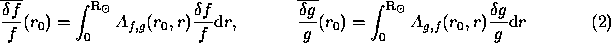
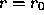 .
The spatial resolution of the averages can be characterized by the central
coordinate and the resolution scale of the averaging kernels. These quantities,
`centre' and `spread', usually represent some integral measure of the kernels
in order to account for effects asymmetry and sidelobes.
.
The spatial resolution of the averages can be characterized by the central
coordinate and the resolution scale of the averaging kernels. These quantities,
`centre' and `spread', usually represent some integral measure of the kernels
in order to account for effects asymmetry and sidelobes.

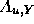 , that
are linear combinations of the corresponding seismic kernels
, that
are linear combinations of the corresponding seismic kernels 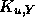 ; b)
Optimally localized averages of the difference
; b)
Optimally localized averages of the difference 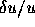 between proxy model 4 and
reference model 1 of Christensen-Dalsgaard et al. (1993)
inferred from the adiabatic frequency differences of the mode set defined
in the text, and the error estimates of IPHIR and BBSO data.
The horizontal bars represent the resolution lengths
(widths of the averaging kernels); the vertical bars represent standard
errors. The dotted curves are the actual differences. (Gough & Kosovichev, 1993)
between proxy model 4 and
reference model 1 of Christensen-Dalsgaard et al. (1993)
inferred from the adiabatic frequency differences of the mode set defined
in the text, and the error estimates of IPHIR and BBSO data.
The horizontal bars represent the resolution lengths
(widths of the averaging kernels); the vertical bars represent standard
errors. The dotted curves are the actual differences. (Gough & Kosovichev, 1993)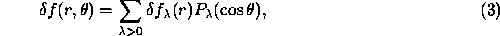
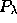 are Legendre polynomials. In this case radial functions
are Legendre polynomials. In this case radial functions
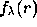 are determined by inverting so-called `a-coefficients',
expansions of the symmetrical part of split-multiplet frequencies into
a set of orthogonal functions of azimuthal order m. The integral equations
relating the even a-coefficients to
are determined by inverting so-called `a-coefficients',
expansions of the symmetrical part of split-multiplet frequencies into
a set of orthogonal functions of azimuthal order m. The integral equations
relating the even a-coefficients to 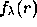 are essentially
identical to Eq. (1) (e.g. Gough, 1993). Therefore, it is proposed to develop
a unified inversion procedure for determining spherical and aspherical
components of the solar structure.
are essentially
identical to Eq. (1) (e.g. Gough, 1993). Therefore, it is proposed to develop
a unified inversion procedure for determining spherical and aspherical
components of the solar structure.