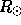The main objectives of the Program is development of the Medium-l Program for basic helioseismological observations using the 5 kbs telemetry channel, which includes development of observational schemes and the pipeline for the data analysis.
The low-rate telemetry channel will transmit only about 3% of the high-resolution data that can be obtained by the instrument on board of spacecraft. However, the channel will operate continuously during the SOHO mission, and therefore it is very important to acquire maximally useful information in order to achieve the scientific goals of the mission.
The observational scheme, which is currently being implemented into the IP on-board software, is based on binning the high-resolution data into a single grid of lower-resolution bins, the total number of which is determined by the 5 kbs rate of the telemetry channel. The further analysis, which includes decomposition of the data onto solar mode eigenfunctions and subsequent time-series analysis, will be carried out at the SSSC. Therefore the binned data should provide maximum information about the eigenfunctions. The problem, therefore, is to design the optimal data binning (optimal masks) for a prescribed number of bins; that number is about 20 000, and depends on the effectiveness of the on-board data compression. Optimal binning schemes have not yet been designed. Their development depends on the observational tasks of the Medium-l Program.
Three different tasks are considered. The first one is to obtain
data from which all eigenmodes of relatively moderate degrees, e.g., up to 100
- 150, can be isolated as cleanly as possible. These data will provide
information about the internal structure and rotation of the sun in the radial
interval 0 - 0.97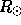
. Perhaps, the simplest approach to this task is to apply a
uniform set of equal bins.
The two other tasks are based on targetting modes of higher degrees in some
specific intervals of angular degree and order. One of the purposes of these
tasks is to obtain detailed information about the structure and dynamics of the
HeII ionization zone, which is located in a narrow region in the vicinity of
0.985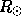
. This information can be obtained by measuring modes of degrees
from 200 to 300, whose lower turning points span this zone. The higher-degree
data would be used to study the physics of the solar plasma under conditions
that are difficult to achieve in the laboratory, and to measure the abundance of
helium in the convection zone, knowledge of which is important for our
understanding of stellar evolution, for testing cosmological models, and for
studying the distribution of helium in the heliosphere. These data could also
shed light on the formation and dynamics of coherent convective motions.
They would also provide boundary conditions for structure and rotation
inversions. Another helioseismological problem is the continuous monitoring of
subsurface convection by observing high-degree sectoral modes. Such measurements
are important for understanding solar
convection and its interaction with rotation and the magnetic field. One of the
possible approaches to accomplish these tasks is to apply a nonuniform binning
scheme similar to ones that have been suggested by Gough (1992) and by
Kosovichev (1992). A nonuniform binning scheme could provide
substantially better resolution of eigenfunctions of modes of higher l (about
300 and above) if the binning were applied to Doppler images that have been mapped
onto heliospheric coordinates. Such mapping, commonly referred to in this
context as remapping, would also give us the ability to investigate in some
detail the structure of mode eigenfunctions, which is essential for studying
nonaxisymmetric asphericity, and to target particularly interesting groups of
modes more precisely.
The data-binning schemes contain an option to filter out small-scale noise and aliases of high-degree modes by applying Gaussian smoothing to the high-resolution images in the binning procedure on board. However, such smoothing will reduce the potential to study modes of higher degrees (200 - 300).